以前学过人工智能算法,但是只是做了比较简单的项目像手写识别和猫狗识别等等,对算法掌握的比较浅显,一直以来特别想做一个能够做一个能够识别自己的小程序,感觉很酷,小牛希望通过这个项目继续深入学习研究相关算法,本系列文章仅记录笔者从小白开始的学习历程。
人脸识别是什么?
人脸识别,特指利用分析比较人脸视觉特征信息进行身份鉴别的计算机技术。用摄像机或摄像头采集含有人脸的图像或视频流,并自动在图像中检测和跟踪人脸,进而对检测到的人脸进行脸部识别的一系列相关技术,通常也叫做人像识别、面部识别。
查阅相关资料发现,人脸识别的关键点是:目标检测,关键点定位,活体检测,相识度度量,人脸属性回归
什么是深度学习?
关于深度学习的前世今生,深度学习属于机器学习的一个分支,机器学习是实现人工智能的一个途径,即以机器学习为手段解决人工智能中的问题。机器学习在近30多年已发展为一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、计算复杂性理论等多门学科。
目前我们人类所讲的人工智能,其实是弱人工智能,其不是能够能真正地推理和解决问题的智能机器,其实是只不过“看起来”像是智能的,也不会有自主意识。 我们通过给它大量的训练数据,让它去学习其这些数据内在的特征和关系,使其能够处理类似训练数据的实际问题。
机器学习中有许多经典的算法,其中有一个叫 人工神经网络 的算法,隐藏层比较多(大于2)的神经网络叫做深度神经网络。而深度学习,就是使用深层架构(比如,深度神经网络)的机器学习方法。深度学习通俗点讲就是神经网络的升级版。
这里简单介绍一下相关概念,大家感兴趣,可以去看一下斯坦福大学公开课:机器学习课程或者这篇文章(小牛感觉写的太牛了,有种通透的赶脚~~)
神经网络如图所示:输入层、隐藏层、输出层
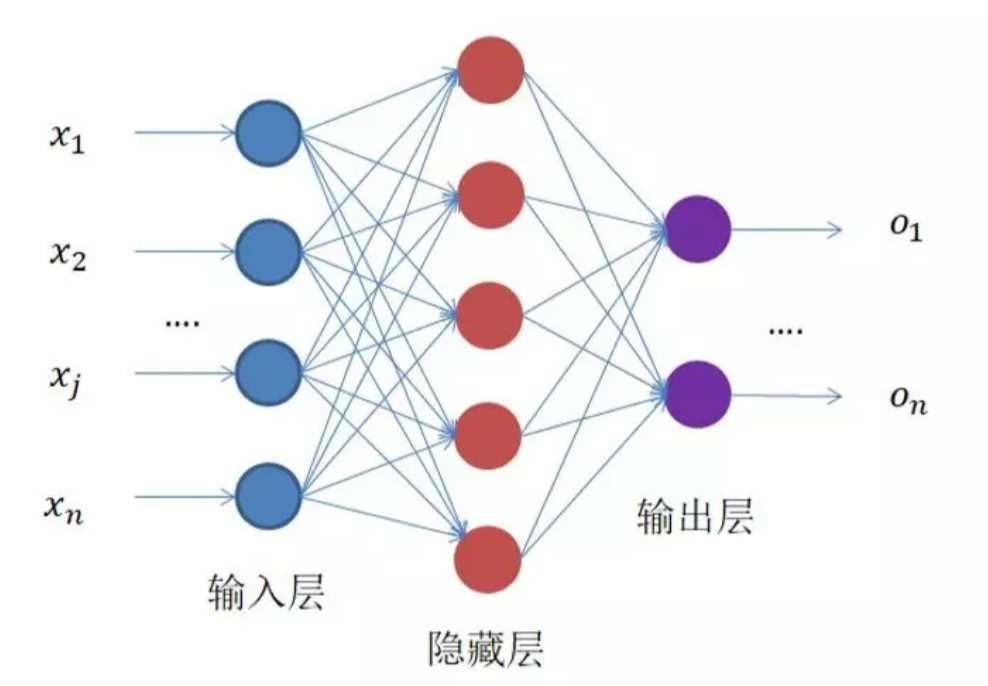
(图片来源网络,侵删)
什么是感知器?
感知器(英语:Perceptron)是Frank Rosenblatt在1957年就职于康奈尔航空实验室(Cornell Aeronautical Laboratory)时所发明的一种人工神经网络。它可以被视为一种最简单形式的前馈神经网络,是一种二元线性分类器。
神经网络的组成单元——神经元。神经元也叫做感知器。
感知器有如下部分:输入权值,激活函数,输出
- 输出权值:一个感知器可以接收多个输入$x_1$,$x_2$... ,一个输入上有一个权值$W_i$,此外还有一个偏置项b。
- 激活函数:感知器的激活函数可以有很多选择,我们选择这个经典的阶跃函数来作为激活函数:
$$f(z) = \begin{cases}
1 & z > 0 \ 0 & z<=0 \end{cases}$$
- 输出:$y=f(w * x + b)$
任何线性分类或线性回归问题,都可以用感知器来解决
多层感知器(MLP)也称人工神经网络(ANN)
深度学习中的概念变迁:神经元->感知器->神经网络->深度学习
前向运算
神经网络的前向运算,就是给定一组输入,计算输出的过程。
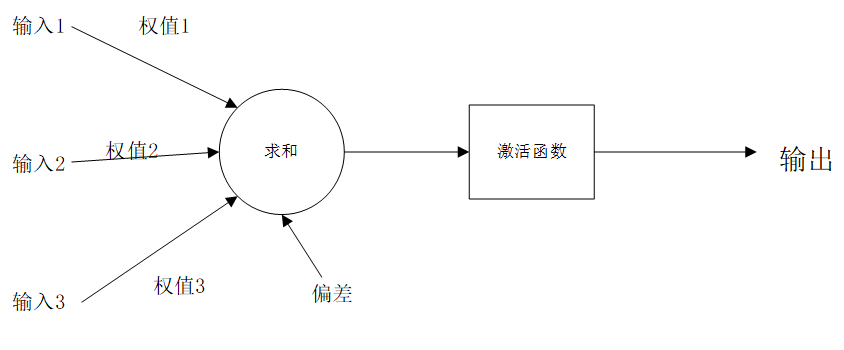
对于前向传播来说,不管维度多高,其过程都可以用如下公式表示:
假设上一层结点输入1,输入2,输入3,…等一些结点与本层的结点有连接,那么本层结点的值就是通过上一层的输入1,输入2,输入3结点以及对应的连接权值进行加权和运算,最终结果再加上一个偏置项(图中为了简单省略了),最后在通过一个非线性函数(即激活函数),如ReLu,sigmoid等函数,最后得到的结果就是本层结点的输出。 最终不断的通过这种方法一层层的运算,得到输出层结果。
$a^2=$ σ($z^2$) = σ($a^1$* $w^2$+$b^2$)
其中,上标代表层数,星号表示卷积,b表示偏置项bias,σ 表示激活函数。
假设我们构造了一个神经网络如下图: 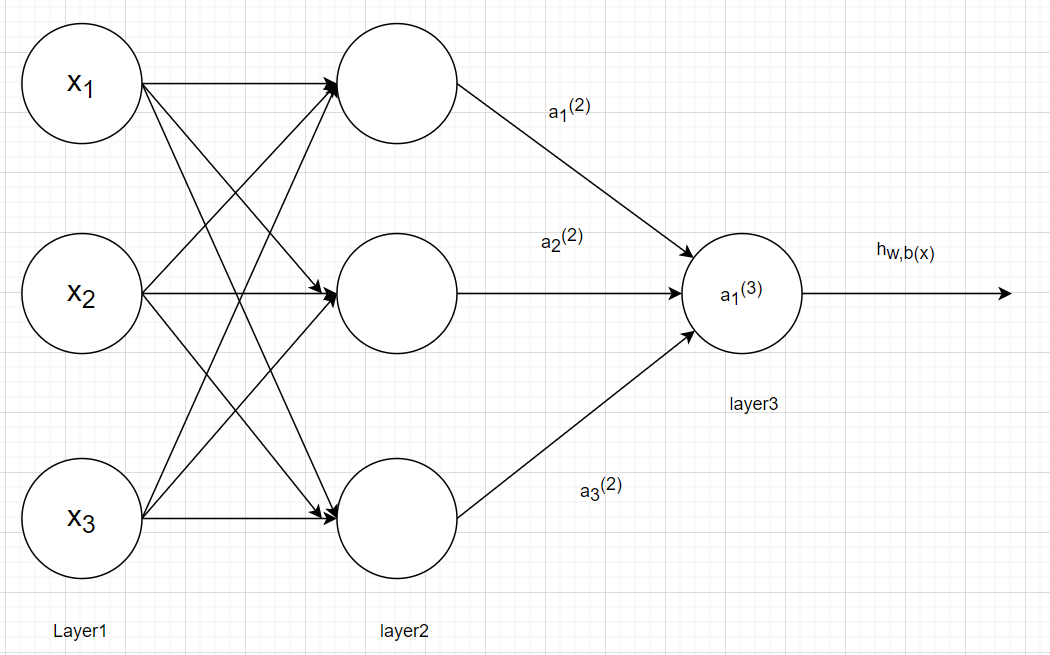
公式如下: 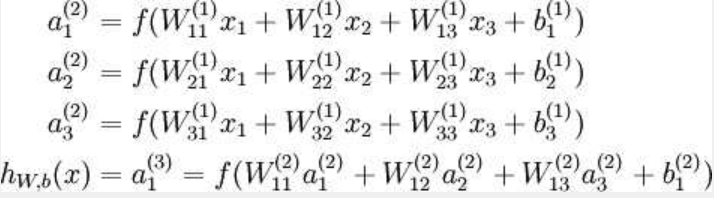
其中f函数是本图规定的算法,Wij就是相邻两层神经元之间的权值,$a_1^2$是对x1,x2,x3进行线性组合,$a_1^3$是都$a_1^2$,$a_2^2$,$a_3^2$的线性组合
如何计算每层权值与偏值,f函数该如何定义,已知具体哪层,求其层的参数是多少?后面文章会一一道来。
明天再继续,概念还是挺抽象的,把概念写明白还是挺累的,脑袋要炸了。
本篇文章到这里就结束啦,如果喜欢的话,多多支持,欢迎关注!
参考:https://www.jiqizhixin.com/graph/technologies/f9849d6c-6262-4c1f-8f42-6d976be17161
https://www.zybuluo.com/hanbingtao/note/433855
https://cloud.tencent.com/developer/news/390591
https://blog.csdn.net/bitcarmanlee/article/details/78819025
本篇文章到这里就结束啦,如果喜欢的话,多多支持,欢迎关注!